Изучая числовые неравенства и их свойства, учащиеся 8 класса столкнулись с задачей, где необходимо сравнить среднее арифметическое, среднее геометрическое и среднее гармоническое некоторых положительных чисел. И если о среднем арифметическом представление имеют все ученики, то что такое среднее геометрическое и тем более среднее гармоническое необходимо пояснить дополнительно.
деленной на количество слагаемых в этой сумме.
2. Среднее геометрическое
положительных чисел x1, x2, ..., xn - число, равное арифметическому корню n-й степени из их
произведения
3. Среднее гармоническое чисел x1, x2, ..., xn - число, обратная величина которого
является средним арифметическим обратных величин данных чисел
Так как ученики 8 класса знакомы только с арифметическим КВАДРАТНЫМ корнем, то и находить величину среднего геометрического мы будем только для двух значений a и b. Советую запомнить эти формулы, а задачу из учебника мы разберём на уроке.


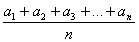


Комментариев нет :
Отправить комментарий
Вы хотите оставить комментарий, но не знаете, КАК? Очень просто!
- Нажмите на стрелку рядом с окошком Подпись комментария.
- Выберите Имя/URL (никто не любит анонимов)
- Наберите своё имя, строчку URL можете оставить пустой.
- Нажмите Продолжить
- В окошке комментария напишите то,что хотели
- Нажмите Публикация.
Если вы хотите разместить изображение в комментарии, то используйте теги [im#]...[/im], вместо точек вставляем URL картинки.
Спасибо!